1、仅有五种正多面体,即是正四面体、正六面体、正八面体、正十二面体和正二十面体。
2、所谓正多面体,当然要首先保证它是一个多面体,而它的特殊之处就在于它的每一个面都是正多边形,而且各个面的正多边形都是全等的。
3、也就是说,将正多面体的各个面剪下来,它们可以完全重合。
 (资料图片)
(资料图片)
4、所以虽然多面体很多,可是正多面体却很少,仅有五个。
5、正四面体是由四个全等的等边三角形组成的;正六面体是由六个全等的正方形组成的;正八面体是由八个全等的等边三角形组成的;正十二面体是由十二个全等的正五边形组成的;正二十面体是由二十个全等的等边三角形组成的。
6、扩展资料:正多面体的相关性质:如果两个正多面体是同类型的正多面体,那么这两个正多面体的二面角都相。
7、2、正多面体的外接球、内切球、内棱切球都存在,并且三球球心重合。
8、3、正多面体的外心、内心、内棱心重合的点称为该正多面体的中心。
9、4、正多面体除正四面体外过任顶点和正多面体中心的直线必然经过正多面体的另一顶点,并且这两个顶点到正多面体中心的距离都相等。
10、5、除正四面体外,连线经过正多面体的f11心的两点称为相财顶点,连两双相对顶点的两条棱称为正多面体的对棱,由对棱围成的两个面称为正多面体的对面。
11、6、除正四面体外,正多面体的对棱、对面都平行。
12、参考资料来源:百度百科-正多面体正多面体的种数很少。
13、多面体可以有无数,但正多面体只有正四面体、正六面体、正八面体、正十二面体、正二十面体五种。
14、证明 顶点数V,面数F,棱数E 设正多面体的每个面是正n边形,每个顶点有m条棱。
15、棱数E应是面数F与n的积的一半(每两面共用一条棱),即 nF=2E -------------- ① 同时,E应是顶点数V与m的积的一半,即 mV=2E -------------- ② 由①、②,得 F=2E/n, V=2E/m, 代入欧拉公式V+F-E=2, 有 2E/m+2E/n-E=2 整理后,得1/m+1/n=1/2+1/E. 由于E是正整数,所以1/E>0。
16、因此 1/m+1/n>1/2 -------------- ③ 说明m,n不能同时大于3,否则③不成立。
17、另一方面,由于m和n的意义(正多面体一个顶点处的棱数与多边形的边数)知,m≥3且n≥3。
18、因此m和n至少有一个等于3 当m=3时,因为1/n>1/2-1/3=1/6,n又是正整数,所以n只能是3,4,5 同理n=3,m也只能是3,4,5 所以有以下几种情况: n m 类型 3 3 正四面体 4 3 正六面体 3 4 正八面体 5 3 正十二面体 3 5 正二十面体 由于上述5种多面体确实可以用几何方法作出,而不可能有其他种类的正多面体 所以正多面体只有5种3.4.6.125种。
本文到此分享完毕,希望对大家有所帮助。
 小狗误食6粒布洛芬器官衰竭死亡!这4种人群建议吃乙酰氨基酚! 【存放好药物! 小狗误食6粒布洛芬器官衰竭死亡 ,医生:药物吸收过多致多器官衰竭】
小狗误食6粒布洛芬器官衰竭死亡!这4种人群建议吃乙酰氨基酚! 【存放好药物! 小狗误食6粒布洛芬器官衰竭死亡 ,医生:药物吸收过多致多器官衰竭】
 华新环保:截至2023年1月20日,我司股东人数为:45,852 华新环保(301265)01月20日在投资者关系平台上答复了投资者关心的问题。
华新环保:截至2023年1月20日,我司股东人数为:45,852 华新环保(301265)01月20日在投资者关系平台上答复了投资者关心的问题。
 驰骋海边!《乐队的海边》感动送别,动力火车苏打酒制造浪漫 心里有期待,就会再见面。本周五中午12:00,全网热播综艺《乐队的海边》第10期如期上
驰骋海边!《乐队的海边》感动送别,动力火车苏打酒制造浪漫 心里有期待,就会再见面。本周五中午12:00,全网热播综艺《乐队的海边》第10期如期上  风范尽显 德华安顾人寿荣获2022年“金智奖”“杰出寿险公司奖” 近日,第十一届金融界领航中国年度论坛暨2022金智奖盛典圆满落幕。作为国内金融行业最
风范尽显 德华安顾人寿荣获2022年“金智奖”“杰出寿险公司奖” 近日,第十一届金融界领航中国年度论坛暨2022金智奖盛典圆满落幕。作为国内金融行业最  海信电视携手《交换人生》爆笑喜乐过新年 2023年兔年春节如果选择一部适合全家一起观看的电影,《交换人生》或许是最适合的一部
海信电视携手《交换人生》爆笑喜乐过新年 2023年兔年春节如果选择一部适合全家一起观看的电影,《交换人生》或许是最适合的一部 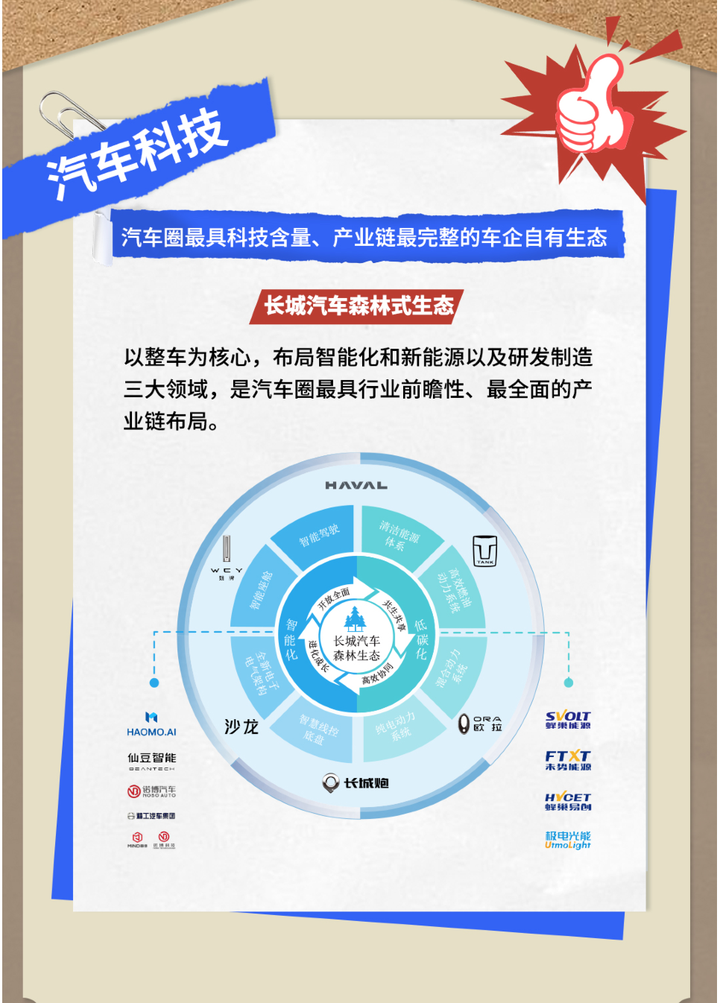 智能化、电动化+完美生态,2022年的长城汽车有多可怕? 尽管汽车行业在转型期竞争激烈,长城汽车近几年的研发实力和多品牌战略的成功也有目共
智能化、电动化+完美生态,2022年的长城汽车有多可怕? 尽管汽车行业在转型期竞争激烈,长城汽车近几年的研发实力和多品牌战略的成功也有目共  一招短线选股法是什么意思?尾盘买入法的好处有哪些?拉尾盘什么意思? 尾盘买入法:属于短线的操作,今天买了,明天就有机会卖的。每天下午14:30分的时候有
一招短线选股法是什么意思?尾盘买入法的好处有哪些?拉尾盘什么意思? 尾盘买入法:属于短线的操作,今天买了,明天就有机会卖的。每天下午14:30分的时候有